What Is Cross-Validation in Machine Learning

Machine learning continues to evolve and penetrate almost every industry, and model accuracy and generalization have become key metrics in determining the success of algorithms. According to a 2025 report by MarketsandMarkets, the global machine learning market size is projected to reach $230.5 billion by 2030, growing at a CAGR of 37.2% from 2023. Amid this explosive growth, data scientists and engineers are constantly seeking techniques that enhance model performance while minimizing overfitting. This is where cross-validation plays a pivotal role.

Cross-validation is a statistical method used to estimate the performance of machine learning models. It allows developers to understand how a model will generalize to an independent dataset, thus ensuring its robustness and reliability. This blog will dive deep into what cross-validation is, its various types, why it's important, its applications across industries, implementation strategies, best practices, and how to go beyond traditional techniques to embrace advanced cross-validation strategies.

What is Cross-Validation?

Cross-validation is a resampling procedure used to evaluate machine learning models on a limited data sample. It provides insights into how a model might perform on unseen data, which is crucial for building predictive models that generalize well in real-world applications.

Instead of splitting the data into one training and one testing set, cross-validation divides the dataset into multiple folds (partitions). The model is trained on a subset of the data and validated on the remaining portion. This process is repeated several times, and the performance metrics are averaged to give a more accurate assessment of the model. In essence, cross-validation mimics the process of testing the model on multiple test sets. It helps avoid the risk of the model being overly optimistic (or pessimistic) based on a single data split.

Why Use Cross-Validation?

Cross-validation addresses a fundamental challenge in machine learning: overfitting. Overfitting occurs when a model performs exceptionally well on training data but poorly on unseen data. This typically happens when the model has memorized the training data rather than learning the underlying patterns.

Benefits of using cross-validation:

• Reduces variance: Helps in reducing the variability of model performance by using multiple validation sets.

• Better model selection: Assists in choosing the best model or algorithm by providing more reliable error estimates.

• Reliable performance estimation: Offers a more truthful understanding of how the model performs in practice.

• Hyperparameter tuning: Cross-validation is essential during grid search or random search for selecting optimal parameters.

• Data-efficient learning: Makes better use of the dataset, especially when the amount of data is limited.

Common Cross-Validation Techniques

Cross-validation plays a pivotal role in assessing the reliability of machine learning models. To maximize its effectiveness, it's important to select the right validation strategy based on the dataset size, structure, and objective. Below are the most commonly used cross-validation techniques in machine learning:

1. K-Fold Cross-Validation

K-Fold is the most popular form of cross-validation. Here, the dataset is divided into k equal parts or "folds." In each iteration, one fold is used for validation while the remaining k-1 folds are used for training. This process is repeated k times, and the results are averaged for a final performance estimate.

• Best For: General-purpose validation with moderate dataset sizes.

• Benefits: Balanced bias and variance; efficient for model evaluation.

• Limitation: May not preserve class distribution in imbalanced datasets.

2. Stratified K-Fold Cross-Validation

Stratified K-Fold ensures that each fold maintains the same class distribution as the overall dataset. This is particularly useful for classification problems where some classes may be underrepresented.

• Best For: Classification with imbalanced class labels.

• Benefits: Maintains class ratios across folds; more stable accuracy estimates.

• Limitation: Slightly more complex to implement than simple K-Fold.

3. Leave-One-Out Cross-Validation (LOOCV)

In LOOCV, each data point is used once as the validation set while the rest of the data is used for training. This process repeats n times, where n is the number of data points.

• Best For: Very small datasets.

• Benefits: Maximum data usage for training; minimal bias.

• Limitation: Computationally intensive; can have high variance.

4. Hold-Out Method

This is the simplest technique, where the dataset is split once into two parts—typically 70–80% for training and the remainder for validation. It’s quick but can give skewed results if the split isn’t representative.

• Best For: Quick performance checks or very large datasets.

  
  

• Benefits: Fast and easy to implement.

• Limitation: High variance; results depend heavily on the random split.

5. Repeated Cross-Validation

Repeated K-Fold performs K-Fold cross-validation multiple times with different random splits. The final result is averaged across all iterations for a more robust performance estimate.

• Best For: When seeking to reduce variance in performance estimates.

• Benefits: More reliable and stable results; reduces the impact of random bias.

• Limitation: Time-consuming; computationally heavier.

6. Time Series Split (Rolling/Expanding Window)

In time-series data, maintaining temporal order is crucial. Instead of random splits, data is split sequentially—where the training set consists of all data before a point, and the test set consists of data that follows.

• Best For: Forecasting and time-series modeling.

• Benefits: Preserves data chronology; realistic scenario testing.

• Limitation: Reduced training data in early folds; more sensitive to trends and seasonality.

Mathematical Foundation of Cross-Validation

Let’s say we use K-Fold cross-validation:

• Total data points = n

• Number of folds = k

In each iteration:

• Train on: (k-1)/k * n data points

• Validate on: n/k data points

Final performance = Average of all validation scores

If EiE_i is the error from the ithi^{th} fold,
CVerror=1k∑i=1kEiCV_{error} = \frac{1}{k} \sum_{i=1}^{k} E_i

This formula provides an unbiased estimation of the model’s performance on new, unseen data.

Implementing Cross-Validation in Python

from sklearn.model_selection import cross_val_score, KFold

from sklearn.ensemble import RandomForestClassifier

from sklearn.datasets import load_iris

# Load data

iris = load_iris()

X, y = iris.data, iris.target

# Initialize model and cross-validator

model = RandomForestClassifier()

kfold = KFold(n_splits=5, shuffle=True, random_state=42)

# Evaluate using cross-validation

results = cross_val_score(model, X, y, cv=kfold)

print("Cross-Validation Scores:", results)

print("Average Score:", results.mean())

This implementation provides a clear and concise way to evaluate your models, adjust hyperparameters, and compare different algorithms.

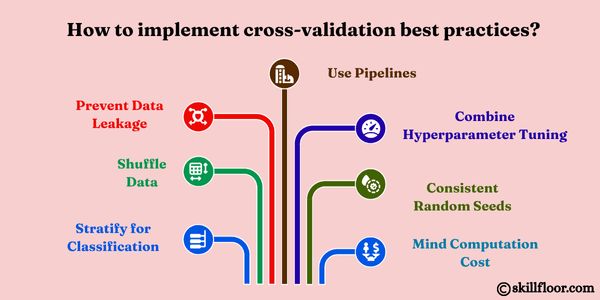
Best Practices in Cross-Validation

To ensure accurate and meaningful evaluation of machine learning models, practitioners should follow these cross-validation best practices:

• Stratify for Classification: Use stratified folds to maintain class distribution, especially with imbalanced datasets.

• Shuffle Data When Appropriate: For non-sequential data, shuffling before splitting helps prevent biases.

• Prevent Data Leakage: Always perform preprocessing steps (like normalization or encoding) within each training fold, not on the entire dataset.

• Use Pipelines: Encapsulate preprocessing and modeling into a single pipeline to ensure consistency during CV.

• Combine with Hyperparameter Tuning: Integrate cross-validation with grid search or randomized search for better model optimization.

• Consistent Random Seeds: Use fixed random states for reproducibility across experiments.

• Mind the Computation Cost: Choose the appropriate CV method that balances accuracy with time and resource usage.

Following these best practices can significantly improve the reliability of your model evaluation and lead to better decision-making.

Limitations of Cross-Validation

While cross-validation is an essential tool for model evaluation, it does have limitations:

• Computational Overhead: Running multiple training-validation cycles can be time-consuming and resource-intensive, especially for large datasets or complex models.

• High Variance with Small Data: In smaller datasets, different data splits can lead to significant variations in model performance.

• Not Ideal for Time-Series Data: Randomly splitting time-series data breaks temporal dependencies. Specialized validation, like forward chaining, is more appropriate.

• Overfitting to Validation Sets: Excessive tuning using CV can lead to models that perform well on validation folds but generalize poorly on new, unseen data.

Being aware of these limitations allows data scientists to choose the right validation strategy and avoid misleading conclusions.

Use Cases Across Industries

Cross-validation plays a pivotal role in ensuring machine learning models are robust and generalizable across various domains. Here’s how it adds value in different industries:

Healthcare

• Disease Diagnosis: Models trained on patient data can overfit easily. Cross-validation ensures diagnostic tools like image classifiers and lab-test predictors remain accurate across populations.

• Patient Readmission: Predictive models estimating readmission risks benefit from K-Fold CV to avoid bias due to unbalanced hospital datasets.

Finance

• Credit Scoring: Stratified cross-validation is essential for ensuring fairness and consistency when modeling risk across diverse borrower groups.

• Fraud Detection: High-class imbalance in fraud cases makes techniques like Stratified K-Fold crucial for evaluating model sensitivity.

Retail

• Demand Forecasting: Cross-validation validates time-series forecasting models, ensuring robust predictions for inventory and supply chain planning.

• Customer Segmentation: Evaluating clustering algorithms with CV ensures insights remain stable across different time periods and datasets.

Manufacturing

• Predictive Maintenance: Time-based CV helps validate models forecasting machinery failure, preserving chronological integrity.

• Quality Control: Cross-validation supports accurate classification of defective vs. non-defective units.

Marketing

• Lead Scoring: Cross-validation ensures the lead prioritization model generalizes across different campaign types and customer journeys.

• Campaign Effectiveness: Repeated CV validates regression models predicting ROI or customer lifetime value.

By tailoring cross-validation strategies to domain-specific challenges, industries can build models that are both powerful and trustworthy.

Advanced Topics

Nested Cross-Validation

Used for model selection and hyperparameter tuning simultaneously. It avoids the leakage that may happen when test data influences parameter tuning.

Bayesian Cross-Validation

Incorporates uncertainty in model evaluation and is particularly useful in probabilistic modeling environments.

Cross-Validation with Pipelines

Ensures that preprocessing steps are included in the validation loop, thereby avoiding data leakage and giving more realistic performance estimates.

from sklearn.pipeline import Pipeline

from sklearn.preprocessing import StandardScaler

pipeline = Pipeline([

    ('scaler', StandardScaler()),

    ('model', RandomForestClassifier())

])

scores = cross_val_score(pipeline, X, y, cv=5)

print("Pipeline CV Score:", scores.mean())

Cross-Validation for Deep Learning

In deep learning, cross-validation is less common due to computational intensity, but when used, it follows similar principles with careful control over randomness and initialization.

Cross-validation remains a cornerstone of modern machine learning workflows. As the global reliance on AI and ML increases, the ability to build reliable, generalizable models is more critical than ever. From preventing overfitting to enhancing model selection, the challenges that cross-validation helps solve are both fundamental and impactful.

Whether you're a beginner or an expert, incorporating cross-validation into your model development pipeline will lead to better, more robust predictions. As machine learning continues to scale new heights in 2025 and beyond, mastering cross-validation will be a vital skill for every data scientist, analyst, and engineer. Stay curious, keep validating—and let your models speak through performance!